Recipe: How To Translate A Recursive Function Into An Implicite One
In order to determine the runtime of a recursive function, it is helpful to translate this function into an implicite one. This blog post illustrates a straight-forward approach, intuitively – with exactly 5 steps on a small example. This approach is also applicable for almost every recursive function.
Why Tho?
The reason to resolve a recursive function lies in the analysis and application. When interested in runtime analysis, the implicite function will serve as a guidance for the total runtime of the recursive function. When interested in application, the implicite function will have the same
results for the same input, but mostly with way less calculation overhead. Transferring a recursion might be a burden, but is effective nonetheless.
An Overview Of The Recipe
First, I want to give you guys an overview of the five steps I mentioned:
- Find a general pattern of behaviour.
- Specify the recursive function in the
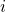 -th step and prove its correctness.
-th step and prove its correctness. - “Find” the end of the recursion, substitute at the
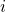 -th step and calculate the result.
-th step and calculate the result. - ???
- Profit.
With these steps, we will be able to overcome this big burden.
The Example
For our transition today, consider this small, cozy example:
(1) ![]()
Small and cozy? Yes. Because I state that the result can be “seen” with a practiced eye almost instantly. We will start with the first step – what is the general pattern? How does this recursion “behave”?
1. The general pattern
We are interested in the behaviour of the recursive scheme. So, lets unfold it and see, what happens:
(2) 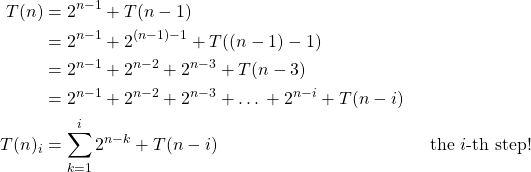
2. Specify the recursive function in the 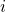 -th step and prove the correctness
-th step and prove the correctness
In the last equation, we recognize a general pattern for the recursion in the ![]() -th step. Lets check, whether its valid:
-th step. Lets check, whether its valid:
(3) 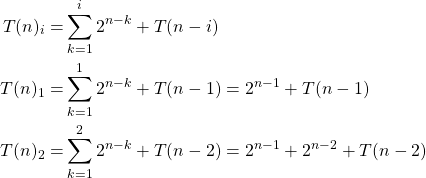
Hm, looks fine to me. But unfortunately, this is not a formal proof of correctness! I just wanted to validate if this makes any sense. Now, we are all set to proof its correctness formally. How? With the tool of mathematical induction (Vollständige Induktion) over ![]() .
.
Let’ summarize the mathematical induction (vollständige Induktion) again. For convenience, at first in english, then in german.
Mathematical Induction In English
- Base case: This is the point of validation for one value of
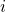 , generally valued in where we want the statement begin to hold with increasing
, generally valued in where we want the statement begin to hold with increasing 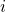 . For the small, cozy example, the base case is
. For the small, cozy example, the base case is 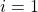 .
. - Induction hypothesis: Here, we assume the validity for the statement for
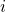 .
. - Induction step: Here, we prove the correctness in the
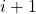 -th step, using the hypothesis in a suiting equation.
-th step, using the hypothesis in a suiting equation.
Vollständige Induktion auf Deutsch
- Induktionsanfang: Der IA ist dafür da, um wenigstens eine Gültigkeit zu sehen. Werte einsetzen, bestens, wo die Induktion anfängt, in unserem Fall
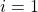 (ein Rekursionschritt). Haben wir oben schon gesehen, passt.
(ein Rekursionschritt). Haben wir oben schon gesehen, passt. - Induktionsvoraussetzung: Die IV beinhaltet die Annahme, dass die Aussage stimmt für ein gewissen Index. Nennen wir den Index mal
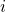 . ‘Bis dahin’ sei die Aussage richtig. Dies schreibt ihr kurz in einem Satz hin, dass das gilt.
. ‘Bis dahin’ sei die Aussage richtig. Dies schreibt ihr kurz in einem Satz hin, dass das gilt. - Induktionschritt: Unter der Tatsache, dass die Aussage stimmt für
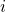 , ist zu zeigen, dass sie auch richtig ist für den Nachfolger der Zahl. Wir schauen uns
, ist zu zeigen, dass sie auch richtig ist für den Nachfolger der Zahl. Wir schauen uns 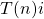 an, verwenden irgendwie die IV und wollen dann aufs richtige Ergebnis kommen.
an, verwenden irgendwie die IV und wollen dann aufs richtige Ergebnis kommen.
The proof
- Base case:
For the base case, we evaluate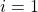 . We get:
. We get: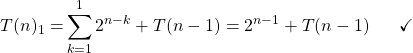
- Induction hypothesis:
It is assumed that the statement holds for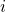 . We now have to prove that it will also hold for
. We now have to prove that it will also hold for 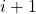 .
. - Induction step:
(4)
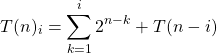
The hypothesis states that this is correct. Now, we apply one more recursion unfolding / unrolling and will see, that it still holds.(5)
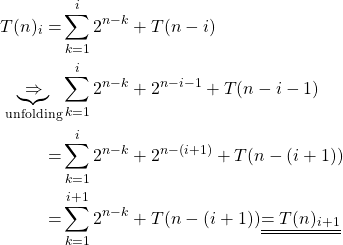
Great! We now have proven, that the statement follows for ![]() , assuming, that its correct for
, assuming, that its correct for ![]() and then by the domino effect, it is proven for all
and then by the domino effect, it is proven for all ![]() !
!
3. Find the end of the recursion, substitute and get the implicite function
If we start at ![]() and decrement by 1 in every recursion, then, the depth of recursion values
and decrement by 1 in every recursion, then, the depth of recursion values ![]() . Quite simple, right?
. Quite simple, right?
(6) 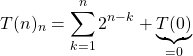
Now, finalize the result! Use the geometric sum to get the following expression:
(7) 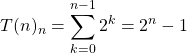
Now, we got the implicite form of ![]() and know in analysis, that the recursion is in fact an exponential function. The calculation takes place in
and know in analysis, that the recursion is in fact an exponential function. The calculation takes place in ![]() instead of
instead of ![]() .
.
4. ???
If the reader were in a situation, in which this task was to be fulfilled in some sort of exam, then this kind of recipe will surely bring some success. Then, the last step also holds:
5. Profit.
How could we have “seen” the implicite result in the recursion itself? We somehow sum up 2 to the power of ![]() , where
, where ![]() traverses from
traverses from ![]() to 1. This is how binary calculation works. This is the bit representation:
to 1. This is how binary calculation works. This is the bit representation:
(8) ![]()
Thanks for reading and as always, stay safe 🙂

